Working on a tough science or math problem can feel like trying to build a bridge while you’re still sketching the blueprint.
When the usual tricks stop working, you need reliable tools, reference points, and communities that help you test ideas quickly.
Below is a guide to some of the best online places to research, compute, check, and present solutions.
You’ll also see tips on how to stitch them together into a repeatable workflow that actually works in practice.
Building a Practical Workflow Before Opening Links

Before jumping into a dozen tabs, it helps to start with a short plan. Most professionals who solve difficult math or science problems follow a similar rhythm:
- Clarify your goal. Define the inputs, unknowns, assumptions, and the type of answer you’re after: an exact formula, a bound, a numerical value, a counterexample, or a proof outline.
- Scan trusted references. Search for names, standard forms, special functions, and known theorems to avoid reinventing the wheel.
- Prototype quickly. Try a symbolic or numeric sketch. If it behaves as expected on simple cases, scale up.
- Search the literature. If the problem feels like a known class, find papers, review articles, or problem books.
- Peer review your idea. Use expert communities to stress test assumptions or edge cases.
- Reproduce and document. Keep a notebook, dataset links, solver versions, and random seeds so others can repeat the result.
Reference Libraries for Definitions, Identities, and Special Functions
The backbone of any problem-solving session is a solid reference source. When special functions or obscure constants show up, a trusted encyclopedia can save hours.
NIST Digital Library of Mathematical Functions (DLMF)
DLMF covers definitions, notation, identities, asymptotics, and numerical methods for functions used across applied math and physics. Each chapter contains “Software” and “Tables” links that connect formulas to computable routines.
It’s actively maintained and versioned, so you can cite a specific release in your notes.
Wolfram MathWorld and Wolfram Functions Site
- MathWorld – https://mathworld.wolfram.com/
- Functions Site – https://functions.wolfram.com/
MathWorld is a broad encyclopedia with cross-linked entries, proofs, and diagrams. Its companion Functions Site catalogs thousands of special functions with curated references. Both are excellent for sanity checks and quick identity lookups while you compute.
Encyclopedia of Mathematics (EMS Press)
https://encyclopediaofmath.org/
A rigorous encyclopedia with peer-reviewed entries hosted by the European Mathematical Society. Great for advanced topics, classical theorems, and precise historical references.
OEIS and LMFDB
- OEIS – https://oeis.org/
- LMFDB – https://www.lmfdb.org/
OEIS recognizes integer sequences, suggests formulas and generating functions, and points to relevant literature.
LMFDB excels at number theory objects such as L-functions, modular forms, and elliptic curves, with searchable invariants and cross-links.
Computation and Computer Algebra

Once you know what you’re dealing with, you need software that crunches numbers, symbols, or both. The tools below cover everything from quick integrals to industrial-scale optimization.
Wolfram|Alpha and the Wolfram Language
- Wolfram|Alpha Step-by-Step – https://www.wolframalpha.com/pro/step-by-step-math-solver
- Differential equations examples – https://www.wolframalpha.com/examples/mathematics/differential-equations
- Wolfram Language DE guide – https://reference.wolfram.com/language/guide/DifferentialEquations.html
Great for symbolic derivations, exact transforms, and step-by-step pedagogy. Pro features show the steps for many problem classes, including calculus, algebra, and differential equations.
Use it for rapid prototyping of transforms, integrals, ODE boundary problems, eigenproblems, and visualizations.
Python’s Scientific Stack: NumPy, SciPy, and SymPy
- NumPy – https://numpy.org/doc/
- SciPy – https://docs.scipy.org/doc/scipy/
- SymPy – https://docs.sympy.org/
Combine NumPy for arrays and linear algebra, SciPy for optimization, integration, statistics, and ODEs, and SymPy for exact symbolic work in pure Python. The three packages are open, well-documented, and used in everything from classroom demos to large research projects.
Optimization Powerhouses: NEOS and COIN-OR
- NEOS – https://neos-server.org/ and user guide https://neos-guide.org/
- COIN-OR – https://www.coin-or.org/ and intro https://coin-or.github.io/user_introduction.html
Global or constrained optimization often benefits from industrial-grade solvers. NEOS routes your model to more than 60 state-of-the-art solvers across linear, integer, nonlinear, and semidefinite programming.
COIN-OR curates open-source solvers and modeling tools such as CBC, IPOPT, and Pyomo.
Interactive Visualization and Simulation
Complex ideas click faster when you can watch them unfold. Browser-based simulations and graphing tools make it easier to spot patterns or errors before formal modeling.
PhET Interactive Simulations
Run simulations across physics, chemistry, and math to build intuition or show results to non-experts. Particularly useful for teaching or presenting.
GeoGebra and Desmos
- GeoGebra – https://www.geogebra.org/
- Desmos Graphing – https://www.desmos.com/calculator
GeoGebra covers geometry, algebra, 3D, and statistics with shareable constructions.
Desmos provides a fast graphing environment, including versions used in major exams, which is helpful when you want a clean, interactive plot to test a hypothesis or show dependencies.
Primary Research and Literature Search
Sometimes the only way forward is to see what the cutting edge has done. The sites below are the quickest paths to high-quality papers and preprints.
arXiv
Machine-readable metadata: https://info.arxiv.org/help/oa/index.html
Open access preprints across physics, math, CS, and more. Use arXiv categories and subject classes to narrow scope, then scan introductions and conclusions for roadmaps and comparisons.
PubMed and PubMed Central
- PubMed – https://pubmed.ncbi.nlm.nih.gov/
- About – https://pubmed.ncbi.nlm.nih.gov/about/
- Help – https://pubmed.ncbi.nlm.nih.gov/help/
PubMed indexes more than 39 million citations with filtering tools and linking to full text where available. The “Help” pages are particularly useful for advanced query tips.
Crossref
- Crossref – https://www.crossref.org/
- Search – https://search.crossref.org/
When you need stable citation metadata across journals, standards, datasets, or preprints, Crossref’s open infrastructure helps locate DOIs and related records.
Add DOIs to your notes as soon as you decide a reference is relevant to make bibliography management easier.
NASA ADS for Physics and Astrophysics
The @SciXCommunity team is attending the annual meetings of BOTH the @ametsoc and @AAS_Office next week. Come visit us in the exhibit halls to learn more about the Astrophysics Data System and the Science Explorer (SciX) expansion. #AAS245 #AMS2025 pic.twitter.com/ODN4QC2nCo
— SAO/NASA Astrophysics Data System (ADS) (@adsabs) January 10, 2025
Indexes millions of records across astronomy and physics with powerful citation analysis. Ideal when your problem touches classical mechanics, relativity, or plasma, and you want canonical references and citation trails.
High-Quality Textbooks and Courseware with Problem Sets
Sometimes you don’t need a research paper-you need a reliable problem set or lecture notes. The following are free and well-organized.
MIT OpenCourseWare
Hosts full courses, problem sets, and exams across physics and mathematics. Look for classic first-year physics and calculus courses which include step-by-step solutions and recitation materials.
OpenStax
- Calculus – https://openstax.org/details/books/calculus-volume-1
- Physics – https://openstax.org/details/books/college-physics-2e
Free, peer-reviewed college textbooks with extensive end-of-chapter exercises. Perfect for structured practice and quick refreshers.
For extra practice beyond MIT OpenCourseWare and OpenStax, check out Qui Si Risolve, which offers solved exercises and clear theory notes for math and physics topics.
Paul’s Online Math Notes
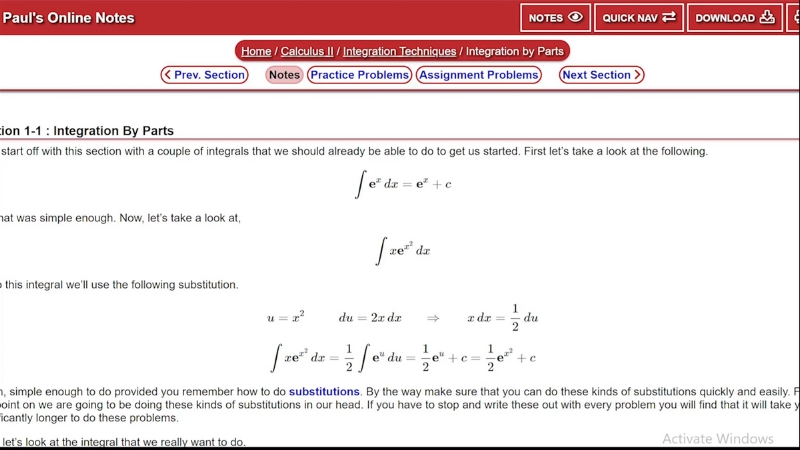
A widely used set of notes and problem banks for algebra, calculus, and differential equations maintained by a Lamar University professor.
Expert Communities for Peer Review of Ideas
Once you’ve drafted a solution, a well-placed question can save days. The Stack Exchange network is the most organized place to do it.
- Mathematics – https://math.stackexchange.com/
- Physics – https://physics.stackexchange.com/
- Cross Validated – https://stats.stackexchange.com/
Show your work, clarify what you tried, and state constraints. You’ll get much better answers and avoid downvotes.
Data, Constants, and Vetted Physical Properties
Accuracy often comes down to the constants you plug in. Use stable, authoritative sources.
- NIST Chemistry WebBook – https://webbook.nist.gov/chemistry/
- CODATA constants – https://physics.nist.gov/cuu/Constants/
NIST hosts authoritative tables with search tools and consistent units. CODATA recommended values are the standard reference for constants used in precise calculations.
Problem Banks and Practice for Sharpening Skills
If you want to sharpen your technique or prepare for contests, a few online problem banks stand out.
- Project Euler – https://projecteuler.net/
- Art of Problem Solving – https://artofproblemsolving.com/
Project Euler offers algorithmic math challenges that force you to combine combinatorics, number theory, and coding to reach scalable solutions.
Art of Problem Solving provides strategy articles and community discussions oriented toward contest-level problem solving.
Three Example Workflows
Below are three common scenarios and how to tackle them.
Special Functions Inside a Differential Equation
- Start with Wolfram|Alpha or SymPy to solve or reduce a differential equation and identify whether a special function arises.
- Look up definitions, domains, and asymptotics in DLMF, then borrow stable expansions for numeric evaluation.
- Produce a numerical benchmark with SciPy’s ODE or special functions modules and cross-check limits against the DLMF forms.
- If the equation is novel, search arXiv for similar forms and solution techniques.
Hard Optimization Model
- Formulate in Pyomo or AMPL, then submit to NEOS to try several solvers without installing locally. Track solver names and versions.
- When you need an open, local solver, look at COIN-OR projects like CBC or IPOPT.
- Validate the objective and constraints on a toy instance, then scale up.
- Re-run on a second solver to check optimality robustness.
Odd Integer Sequence in a Combinatorics Problem
- Paste initial terms into OEIS to identify the sequence and read conjectures or closed forms.
- If you suspect deeper structure, search LMFDB or MathWorld for associated objects and identities.
- Use SymPy to symbolically manipulate generating functions and verify small-n cases.
Quick Chooser Table
| Goal | Best Starting Point | Why It Helps | Follow Up |
| Identify a function or identity | DLMF, MathWorld | Canonical definitions, proofs, tables | Cross-check with CAS output and DLMF normalization |
| Compute or prototype | Wolfram | Alpha, SymPy, SciPy | Rapid exact or numeric results with plots |
| Solve an optimization model | NEOS, COIN-OR | Access to many solvers, open tools for local runs | Record solver versions and compare solutions |
| Search new research | arXiv, Crossref, ADS | Fast access to preprints and stable DOIs | Track citations and versions in your notes |
| Check biomedical literature | PubMed | High-quality indexing and filters | Use MeSH terms and “Similar articles” |
| Build intuition with visuals | PhET, GeoGebra, Desmos | Interactive simulations and graphs | Export images for reports or talks |
Practical Tips to Avoid Common Pitfalls
- Confirm conventions. Many special functions have competing normalizations. Always match definitions between your solver and the reference.
- Be explicit about assumptions. Mention domains, initial conditions, parameter ranges, and regularity. Solvers and CAS often default to principal branches or generic assumptions.
- Check edge cases. Test trivial limits, symmetry cases, and units. A quick Desmos or GeoGebra sketch catches a surprising number of sign mistakes.
- Use stable sources for properties and constants. Pull constants from CODATA and properties from NIST WebBook to avoid inconsistent tables.
- Cite DOIs. When you rely on a paper, add its DOI from Crossref or the arXiv identifier for clarity.
- Respect community rules. On Stack Exchange, well-posed, research-level questions with your own work shown get the best answers.
Final Thoughts

Solving hard math and science problems isn’t about having one magic trick. It’s about assembling the right pieces, a rigorous reference, a capable computation stack, a solid search strategy, and a quick way to visualize or simulate.
Knowing how to tell if online content is reliable is part of choosing those pieces wisely.
The resources above work together naturally. With a tidy workflow and careful notes, you can move from a rough idea to a result you trust and can reproduce.






